How to solve the ripple and noise problems caused by improper inductor selection in SMPS?
2024-05-23 15:05:37 126
1. What is Switching mode power supply
SMPS is an efficient regulator that reduces the input voltage (buck converter), increases the input voltage (boost converter), or does both (buck - boost converter). Figure 1 shows the basic switching converter topology.

Figure 1. Common SMPS topologies and their output formulas
Each SMPS works the same way: storing energy in an inductor and utilizing pulse width modulation (PWM) technology to get the desired output. These converters should follow the law of volt-second equilibrium, that is, when operating at steady state, the average current of the inductor in one cycle must be zero. Therefore, the inductor must discharge all the current stored in the charging phase before another cycle begins.
2. Buck converter operation
This article only uses buck converters to demonstrate common design errors. The power stage of a buck converter consists of the following four components: an inductor, an output capacitor, a top FET (represented by a switch), and a bottom FET (represented by a diode), as shown in Figure 2.
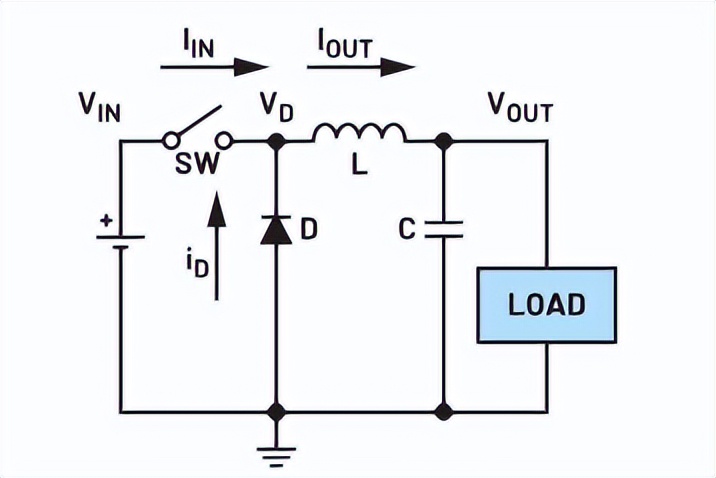
Figure 2. Simplified buck converter power stage
The voltage at both ends of the inductor is calculated by the following formula: VL = L diL/dt. This voltage is the difference between the switching node and the output voltage. When the top FET is on, VL is the difference between the input voltage and the output voltage. When the top FET is off, the difference is 0 V minus the output because the switch node is grounded. diL/dt (or ΔiL) is the change in inductive current over time, often referred to as inductive current ripple. When the top FET is closed (the bottom FET is disconnected), the inductor stores energy in the form of magnetic flux as the current flowing through the inductor increases. When the top FET is disconnected and the magnetic field is lost, the bottom FET will form a ground path, so that the current can still flow to the load in reduced hours. This can be seen in the inductive current waveform shown in Figure 3. The output capacitor is used to obtain a smooth output ripple and to assist in maintaining the desired output voltage. The output voltage of the buck converter is derived from VOUT = DVIN, where D is the duty cycle, defined as the percentage of the total cycle time that the top FET is on and charging the inductor.

Figure 3. Inductive current waveform. When the top FET is on, the current flowing through the inductor is charged. When the top FET is turned off, the current flowing through the inductor is discharged
3. Recommended inductor size
When designing SMPS, the correct inductance value must be selected to ensure that the inductance current ripple (ΔiL) is within an acceptable range. It is recommended that the inductance ripple of the buck converter should be between 30% and 40% of the applied load current. This range is generally considered ideal, as it is sufficient to capture an accurate signal and transmit it to the current mode control feedback system, but not so large as to cause the power supply to enter discontinuous on-mode (DCM). DCM is A state in which the current ripple is so large that it forces the current below 0 A in order to maintain the load current at the desired value. However, once 0 A is reached, the diodes inside the FET are no longer on, preventing the current from dropping below 0 A. The correct inductance selection is generally based on the following formula:

This formula shows that the switching frequency is inversely proportional to the inductance, which means that the higher the frequency, the shorter the charging time, allowing normal operation (saving space and cost) with a smaller inductance.
4. Inductor saturation
A common catastrophic mistake in SMPS design is to ignore the current saturation rating when selecting the power inductor. When the current flowing through the inductor exceeds the saturation current rating, the inductor core is saturated, which means that the magnetic field generated will no longer increase in proportion to the current consumed. This breaks the law of volt-second equilibrium, causing the inductor current ripple and output voltage ripple to lose their linearity. When the core is saturated, the inductance value decreases rapidly and behaves more like a resistance than an inductance. Since the effective series resistance (ESR) of the inductor increases while the actual inductance decreases, the amount of current change will be forced to increase in order to meet the volt-second equilibrium. The spike observed in the saturation current waveform is caused by an exponential increase in the current slope, as shown in Figure 4. This current spike affects the output voltage, resulting in more noise and voltage spikes, as shown in Figure 5. If the voltage spike is too large and exceeds the maximum voltage rating of the downstream component, noise and voltage spikes may damage the downstream component and reduce EMI performance.
 Figure 4. Saturation inductance current waveform. The waveform behaves normally until the current exceeds the saturation rating
Figure 4. Saturation inductance current waveform. The waveform behaves normally until the current exceeds the saturation rating

Figure 5. Saturated inductor output ripple. Spikes continue to the output, which includes noise and voltage spikes
In addition, in the case of large current fluctuations, the inductor will experience rapid hysteresis loss, which causes the inductor to dissipate too much heat (as shown in Figure 6) and produce audible noise. Too much heat can damage other nearby components (especially the regulator chip itself).
 Figure 6. Inductor saturation heat dissipation temperature of 226°F (107.78°C)
Figure 6. Inductor saturation heat dissipation temperature of 226°F (107.78°C)
To avoid this problem, designers should choose an inductor with a rated current at least twice the expected maximum current. When calculating the maximum current, it is important to consider the inductance current ripple and the load current consumed at the output end. In addition, designers can consult the inductor's data manual to find out at what current the inductor value will decrease by 10% to 30%, which is the definition of saturation. Selecting an inductor with an appropriate saturation current rating will allow the system to function properly, as shown by the linear current flowing through the inductor in Figure 7. The output voltage spike will disappear, as shown in Figure 8. Finally, the system will operate at lower temperatures (as shown in Figure 9), reducing the impact on the equipment and extending the service life of the equipment.
 Figure 7. Nominal inductance current waveform
Figure 7. Nominal inductance current waveform
 Figure 8. Nominal inductance output ripple
Figure 8. Nominal inductance output ripple
 Figure 9. Nominal inductance heat dissipation temperature of 99.7°F (37.61°C)
Figure 9. Nominal inductance heat dissipation temperature of 99.7°F (37.61°C)
5. Problems faced by ultra-small inductors
Designers usually prefer to choose inductors with smaller inductance values in order to save space, and such inductors have fewer coils and therefore smaller dimensions. However, if the inductor is too small, the ripple current will be large and will force the converter into DCM mode, which is undesirable for SMPS because the efficiency of the device will be reduced and electromagnetic interference (EMI) performance will be poor. This EMI performance degradation may be observed when the switching node rings, which is caused by parasitic effects and the LC resonant circuit (the circuit that produces the resonance), as shown in Figure 10. This ringing affects the output voltage, resulting in larger ripples and more voltage spikes, as shown in Figure 11. In addition, the power supply is no longer in continuous on-mode (CCM), and the derived SMPS output formula no longer applies.
 Figure 10. Ultra-small inductance output waveform. If the inductive current cannot be obtained, a ringing phenomenon is also observed at the switching node
Figure 10. Ultra-small inductance output waveform. If the inductive current cannot be obtained, a ringing phenomenon is also observed at the switching node
 Figure 11. Ultra-small inductance current waveform. Ringing in current and RSENSE indicates that the power supply is in DCM mode
Figure 11. Ultra-small inductance current waveform. Ringing in current and RSENSE indicates that the power supply is in DCM mode
To solve this problem, designers should choose an inductor that can provide about 30 to 40 percent of the current ripple. This reduces the amplitude of the inductive current ripple, causing the device to return from DCM to CCM mode, as shown in Figure 12. This also improves the output voltage ripple and eliminates voltage spikes, as shown in Figure 8. If designers are having trouble calculating the required inductance values and selecting suitable components, LTPowerCAD can be used to assist in the design and selection of power level components.
 Figure 12. Nominal inductance current waveform
Figure 12. Nominal inductance current waveform
6. Problems faced by large inductors
Downstream electronic components connected to SMPS usually have a specified supply voltage and associated tolerance. If the ripple on the voltage rail is too large, it will seriously affect the operation of the system. For example, if the microcontroller's power supply specification is 3.3V ±50 mV, a ripple greater than ±50 mV may cause the microcontroller to shut down. Designers generally reduce this ripple by increasing the size of the inductor. However, if the inductor size is too large, the current ripple, as well as the output voltage ripple, will be significantly reduced. While this sounds desirable, it can cause problems with the feedback system, and it can also cause a slower transient response. The small ripple will make it difficult for the series detection resistor to detect the change, thus distorting the common triangular waveform transmitted to the feedback loop. When the inductor current ripple is small, the signal-to-noise ratio (SNR) is reduced. This causes the feedback loop to record the noise as an inductor signal, which causes the output signal to be unstable (manifested as jitter), as shown in Figure 13.
 Figure 13. Output instability resulting in jitter. The large inductance output waveform shows a continuous characteristic. The highlighted waveform is captured by nominal inductance
Figure 13. Output instability resulting in jitter. The large inductance output waveform shows a continuous characteristic. The highlighted waveform is captured by nominal inductance
In addition, the larger the inductance value, the smaller the saturation current rating usually is. This can lead to inductance saturation, which is very dangerous for the device, as described in the "Inductor Saturation" section. The influence of ultra-large inductance saturation is shown in Figure 14.
 Figure 14. Saturation inductance output waveform of an inductor whose inductance value is 22 times the nominal value. The rated current does not increase proportionally with the inductance
Figure 14. Saturation inductance output waveform of an inductor whose inductance value is 22 times the nominal value. The rated current does not increase proportionally with the inductance
To mitigate this problem, designers remember that output voltage ripple can be controlled by changing the output capacitance selection. By increasing the value of the output capacitor or decreasing its ESR, the output voltage ripple can be reduced without increasing the value of the inductor. This keeps the inductive current ripple value between 30% and 40%, enabling the detection architecture to obtain the signal correctly. This can be seen in Figure 15.

Figure 15. Nominal detection resistance waveform
7. Overview
This paper can be used as a guide to analyze the design problems of inductors in buck converters. In addition, this paper aims to provide designers with practical solutions to avoid any of the interference behaviors described in the paper. Keeping the inductance ripple in the 30 to 40 percent range of the output by properly resizing the inductance is critical to ensuring that the device remains in the CCM state and does not cause interference jitter or saturation, which can be fatal to the load or the voltage regulator chip itself











